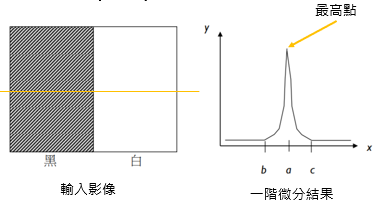
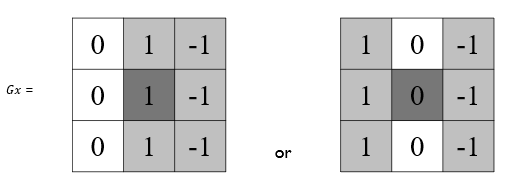
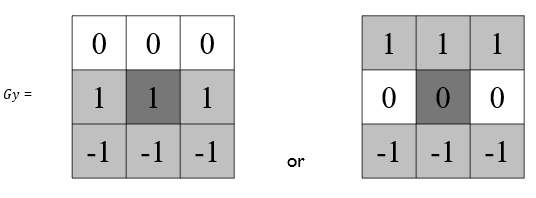
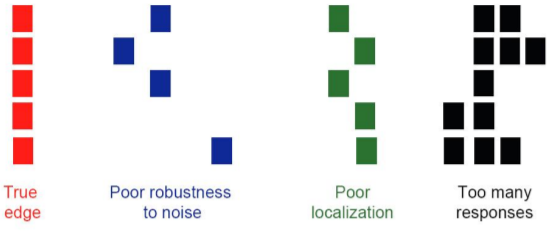
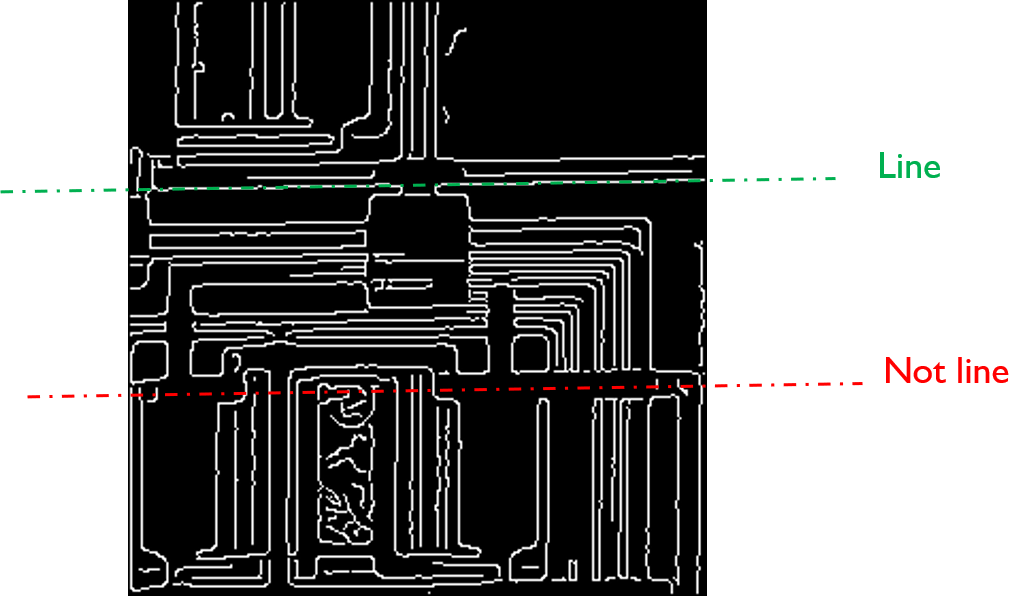
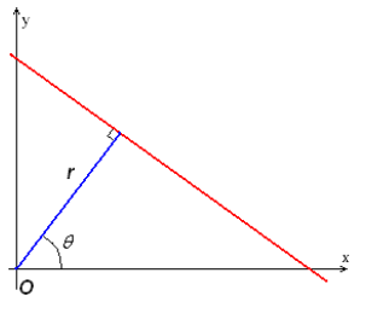
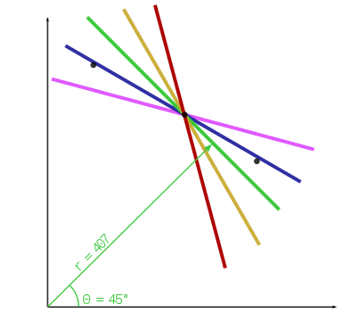
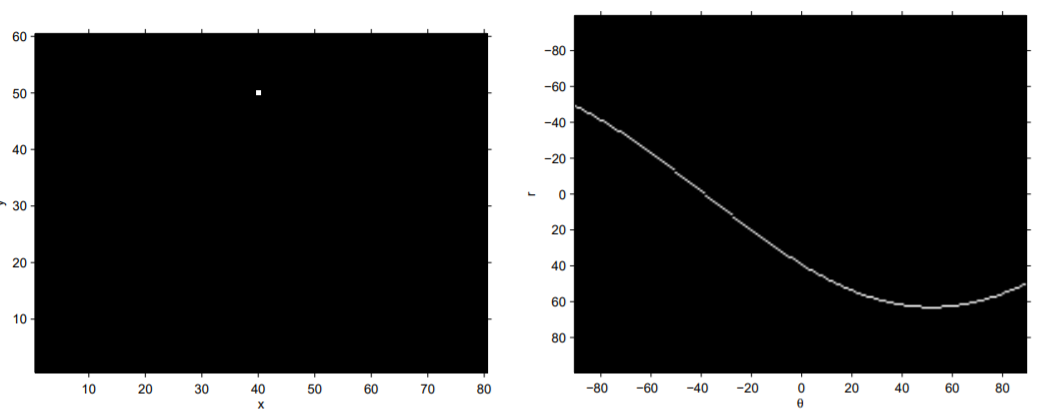
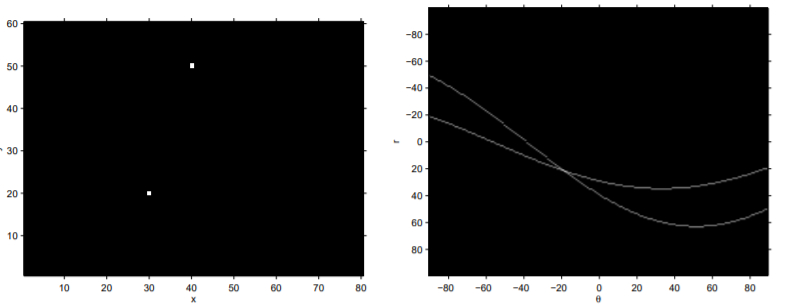
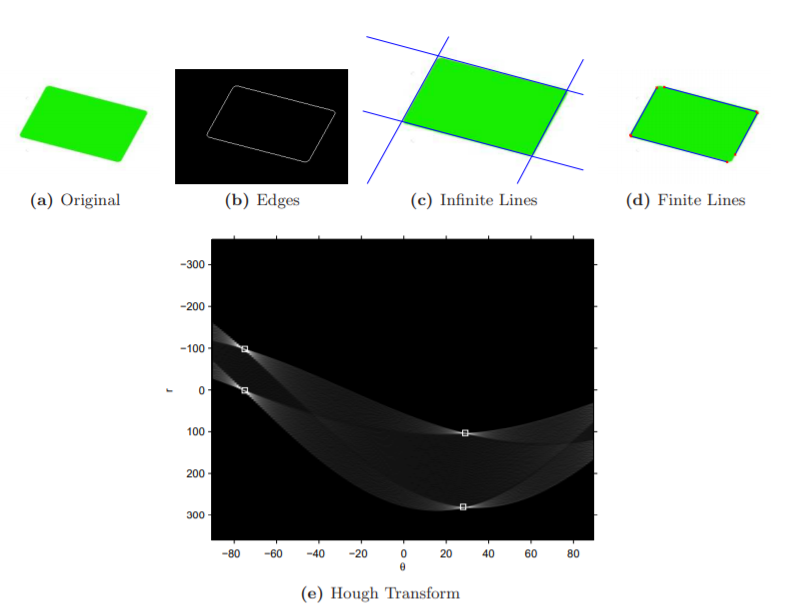
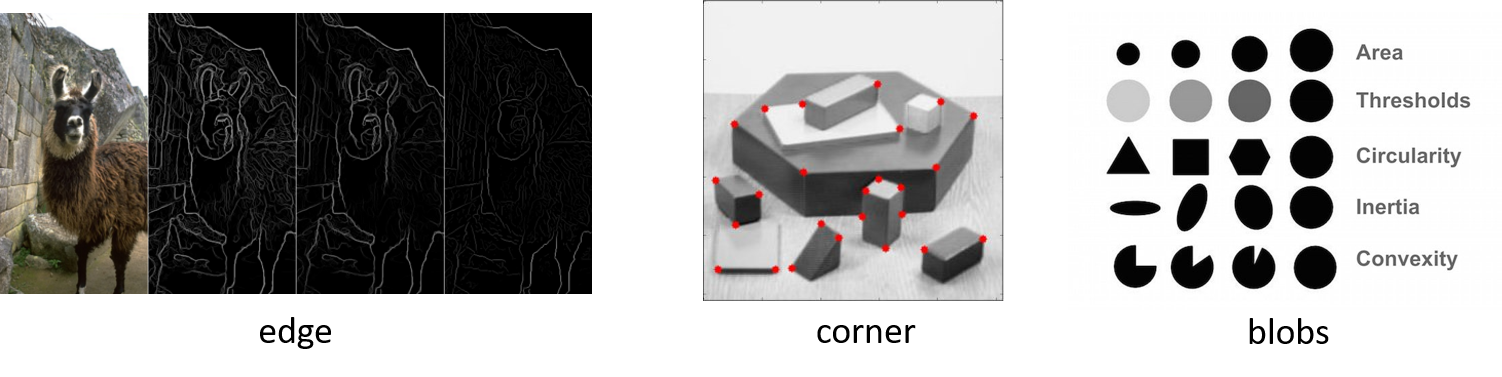
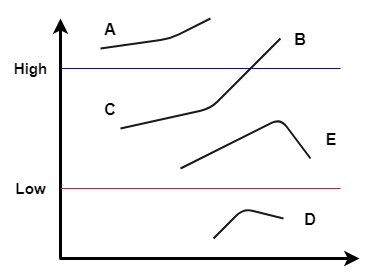
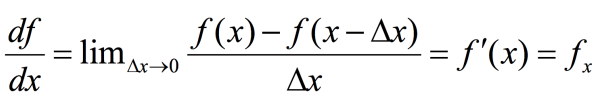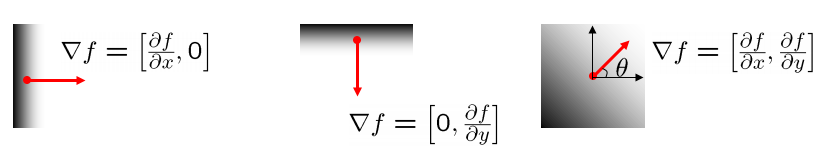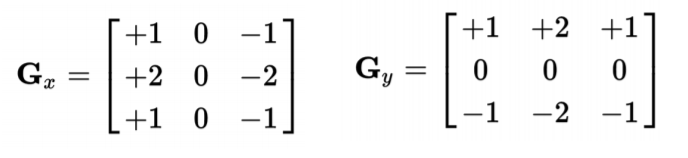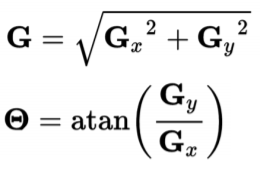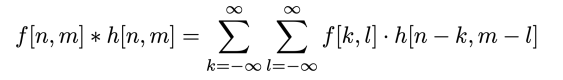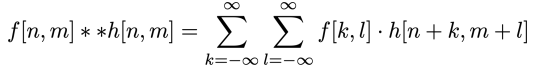線段檢測的難題
- 會有雜訊干擾
- 如何找到一條局部斷裂的線
- 由 noise 干擾導致檢測方向偏移
回顧投票法
- 蠻力投票法,時間複雜度$ O(N^2) $
- 投票法可以讓所有模型通用
- 循環所有參數,取得投票結果
- 選出高票參數結果
- 雜訊所產生的線段也會被納入投票的參數中,但通常結果會與我們想要的預期不符
RANSAC
RANdom SAmple Consensus,隨機抽樣一致
將資料分成 inliers(正常數據), outliers(異常數據)
RANSAC 目標:濾除異常數據,使用正常的數據進行檢測
直覺來看,在線段檢測中,若選擇的 edge 是 outliers 進行擬合時,其他點應該不會在所擬合的線段上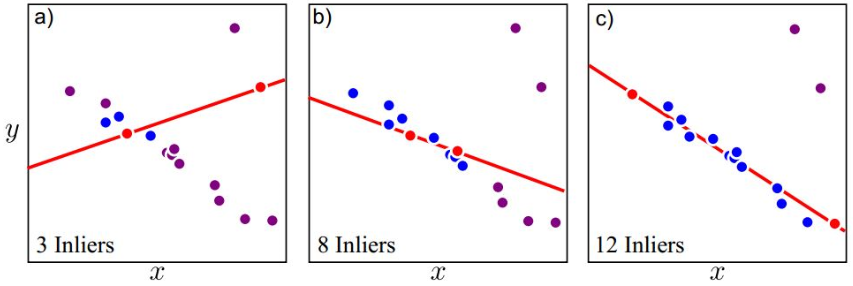
隨機選取兩點得到直線後,藍色點為靠近線段的 inliers,紫色點為遠離線段的 outliers
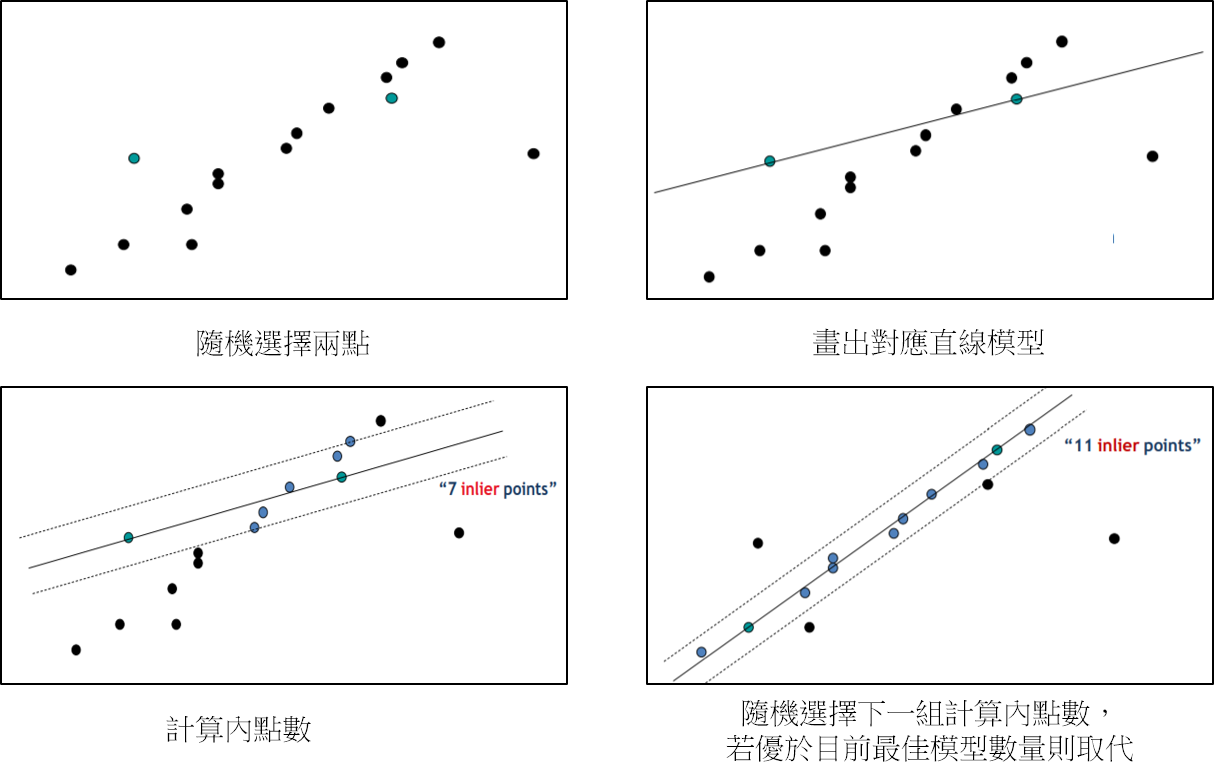
RANSAC 流程
循環 k 次迭代:
- 在一組資料集中(ex:edge 點座標)隨機選擇要執行模型評估的最小數據集(ex:直線偵測下是兩個點)
- 代入選擇的數據集來計算數據模型
- 尋找此模型內的 inliers 數量
- 比較當前模型結果與目前最佳模型結果數量,紀錄最大 inliers 數量與對應模型結果
- 重新估算迭代次數 k
如何設定參數 k
參數符號定義:
- 假設$n$是建立模型所需的點數量(已知,ex:直線擬合需要兩點)
- $w$ 是 inliers 的數量/數據集的總數量(未知)
- $w^n$是所有$n$個點均為是 inliers 的機率
- $1-w^n$是所有$n$個點有一個是 outliers 的機率
- 迭代$k$次都沒辦法找到所有點是 inliers 的機率$(1-w^n)^k$
- 迭代$k$次所有點是 inliers 的機率$1-(1-w^n)^k$
選擇較高的迭代次數$k$來讓找到 inliers 的機率提高
假設演算法跑完$k$次成功機率為$p$
$1-p = (1-w^n)^k$
$p = 1-(1-w^n)^k$
$當n不變時、k越大、p越大,其中p自行定義$
更新迭代次數$k$公式:
$k=\frac{log(1-p)}{log(1-w^n)}$
改善 RANSAC 效率方法:
- 先對資料集進行最小二乘法得到不錯的模型(全局最佳化),再進行 RANSAC(本地最佳化)
RANSAC 優缺點:
- 優點
- 通用方法適合各種擬合問題
- 好實現
- 缺點
- 對於資料集中 outliers 數量變多時,時間成本會大幅提升,真實問題通常都有較大佔比的 outliers(可能的解決方法:隨機選擇資料集中的子集合)
- 非確定性算法:每次跑完結果可能不一樣,但會在一定機率下跑出合理的結果
參考
RANSAC 算法详解(附 Python 拟合直线模型代码)
随机抽样一致(Random Sample Consensus, RANSAC)