k means clustering 流程
- 隨機初始化群心$c_1,…,c_K$與迭代次數$t$
- 計算隸屬矩陣$\delta^t$，得到新的分群結果
- 由分群結果更新群心
- 增加迭代次數$t$，重複步驟2~4，直到到達設定停止條件(到達迭代次數上限或群心不在大幅變動)
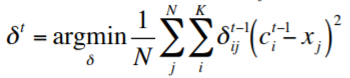
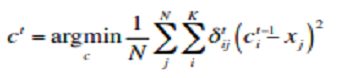
參數定義：
- $t$：迭代次數
- $K$：群數
- $N$：輸入的資料數量
- $x_j$：輸入的第$j$筆資料
- $c^t_i$：第$t$次第$k$群的群心
- $\delta^t$：第$t$次的隸屬矩陣，定義第$j$個資料對應第$c$個群心的距離，矩陣大小為K*N
流程：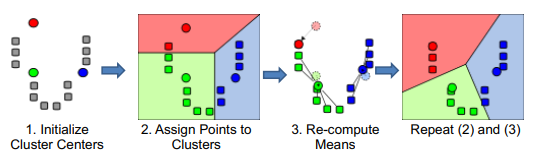
k means clustering特性
- 不同的初始化群心位置會有不同結果
- 對球形的數據有較好的fit結果
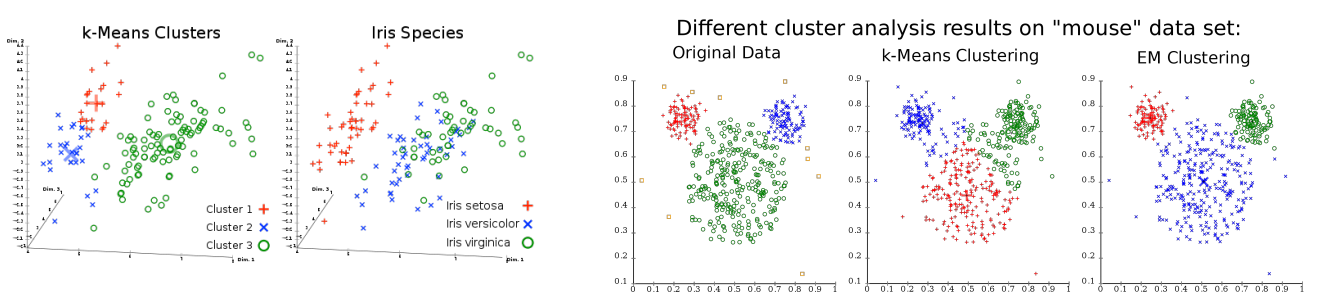* 需要決定參數k
選擇參數k的方法
不同的群數使得結果不同，決定群數變成非常重要的問題
以分群的角度來看，分群的目的為，群內的變異性越小越好，群跟群之間的變異性越大越好
翻成白話來說就是：同一群內的資料越聚集越好，群跟群之間的資料離越遠越好
這裡介紹一個常用來自動選擇群數k的方法：Elbow method
Elbow Method
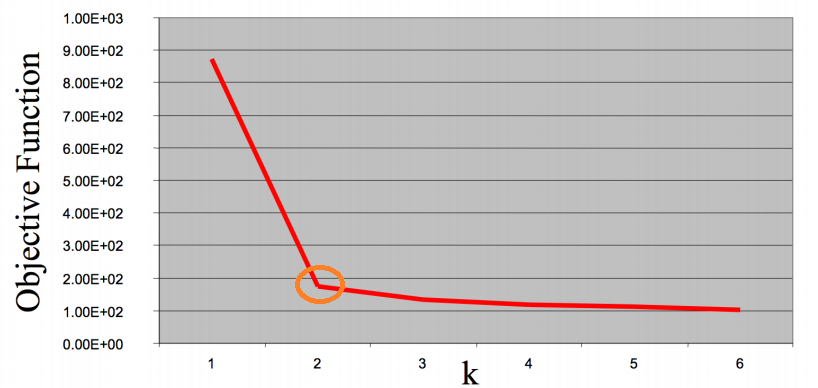
Elbow method的核心思想是，運用前面所說分群的特性來定義一個objective function來找到輸入資料對應最好的分群結果，通常使用群內樣本的距離和來量測
如下圖所示，選擇的k值隨著群數分越多，數值越小，但可以發現前期變化很大，到後面逐漸變小
而群數設定為2時的轉折最大，像是手肘彎曲的地方，這時elbow method就選擇該輸入的資料分為2群最適合
k-means 優缺點
- Unsupervised learning
- 原理簡單好實現
- 可擴展至大型的數據集，適應不同的dataset
- 保證收斂
- 可以預先初始化群心中心
- 需先設定參數k(使用elbow method可以解決這問題)
- 輸入資料需標準化到同一尺度空間
- 初始化群中心影響分群結果
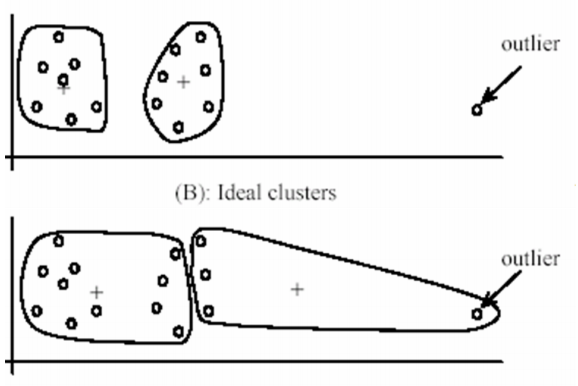
- 群心容易被異常資料(outliers)影響，造成群心偏移
- 容易陷入局部最佳解
