問題
Harris corner 沒有尺度不變性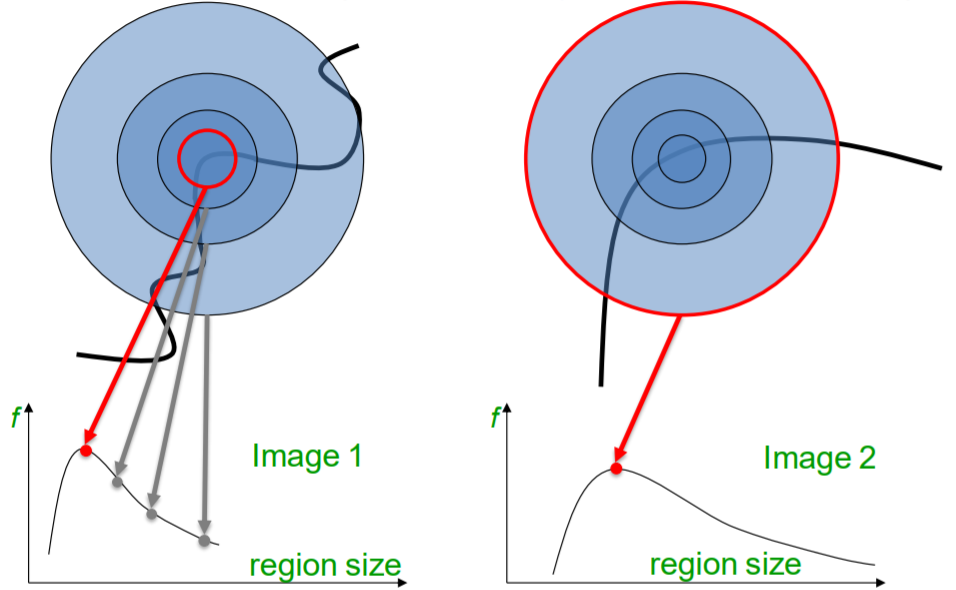
在不同尺度下所呈現的角點響應函數都不同,Image 1 的最小圓圈範圍是跟 Image 2 最大圓圈範圍才會有相同的角點結果
解決方法
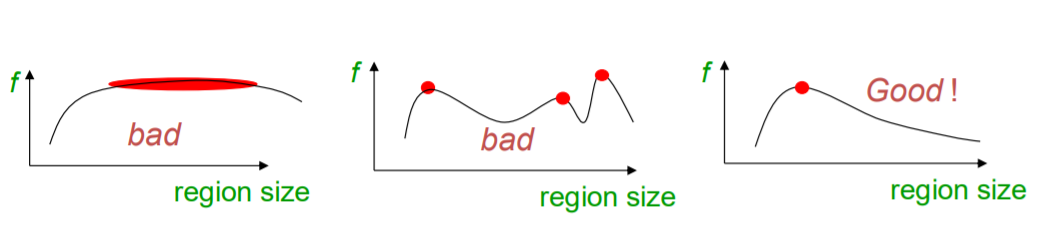
希望能設計一個 scale invariant detection function 可以讓每張影像都找得到一個穩定的尖峰,才能在多尺度搜尋時找到相同的結果
Scale Invariant Detection
使用 Laplacian 與 Difference of Gaussians kernel 來對影像進行不同尺度的縮放
Laplacian kernel
$L = \sigma^2(G_{xx}(x,y,\sigma)+G_{yy}(x,y,\sigma))$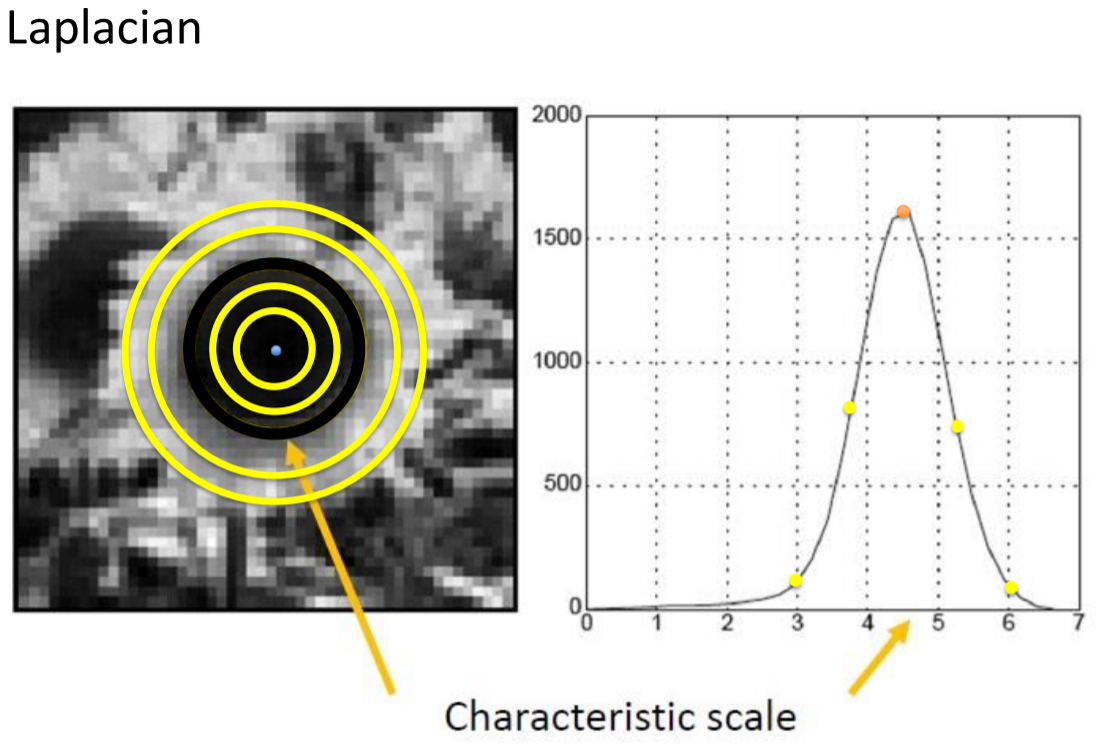
其中 G 是高斯函數
$G(x,y,\sigma)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{x^2+y^2}{2\sigma^2}}$
Difference of Gaussians(DoG)
$DoG = G(x,y,k{\sigma}) - G(x,y,{\sigma}) $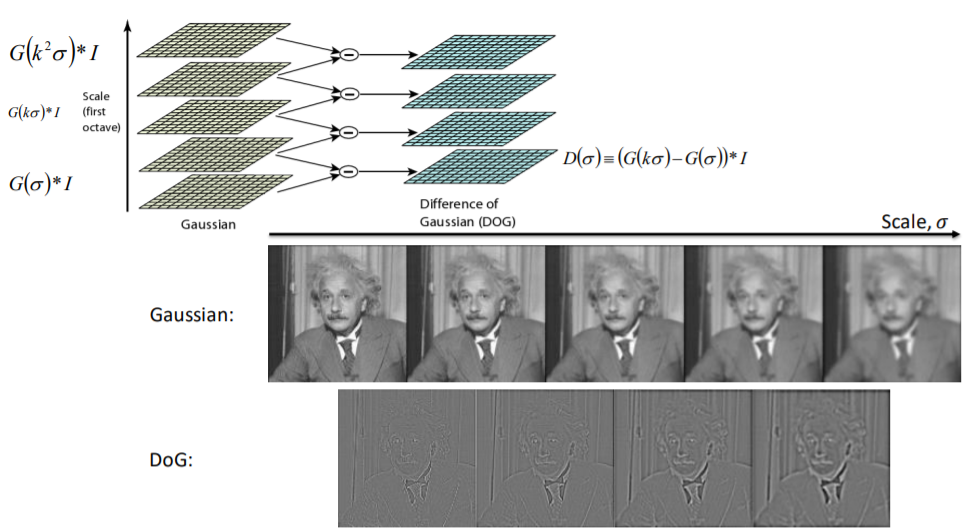
對影像逐漸加深模糊度,越模糊所保留的細節越少
高斯差所得到的影像細節隨著$\sigma$越大細節越粗糙
Scale Invariant Detections

- Harris-Laplacian:結合 Laplacian kernel 的 harris corner,並取出局部最大值作為結果
- SIFT:使用 DoG 並對每個點取 3x3x3 鄰居 26 個點(不包含自己),找出高斯差最小的數值