使用特徵點來尋找物件、定位、全景拼接
使用 Local Invariant Features 動機
- 全局特徵有它的限制性
- 增強對遮擋、角度變化的魯棒性
常見的方法
- 找到多個獨特的關鍵點
- 定義一個 window 大小把 key points 的的周圍資訊取出來
- 提取周圍資訊並做正規化
- 計算正規化區域的局部描述子,例如使用區域色彩資訊
- 匹配局部描述子
好的 Local Features 特性
- 區塊特徵萃取要有重複性與準確性
- 特徵是局部的獨特,對變形與雜亂背景有魯棒性
- 要能萃取夠多的特徵進行比對
- 計算方法越快越好
Harris Corner
設計準則:可以很簡單的用一個小視窗當作視野範圍辨認出角點
如果在角點,往任意方向移動這個小視窗應該會有很大的亮度變化
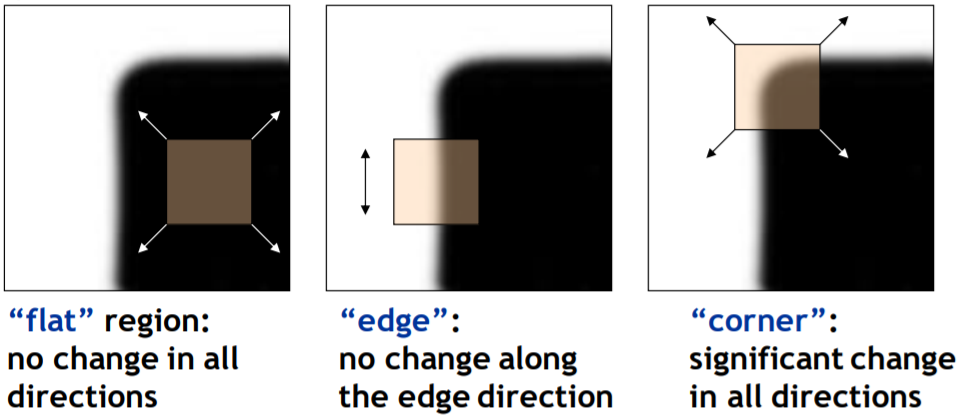
Formulation
移動小視窗的中心座標點$[x,y]到[x+u,y+v]$來計算移動後的亮度變化
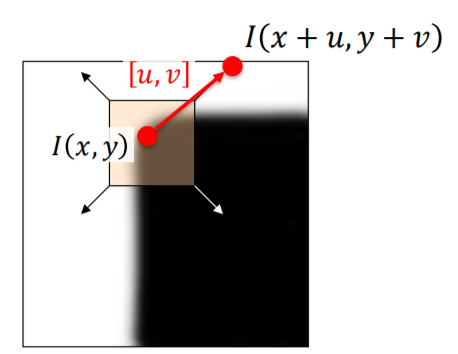
量測單點亮度變化公式:
$ I(x+u,y+v) - I(x,y) $
計算整個小視窗內的亮度變化公式:
$\sum_{xy}w(x,y)[I(x+u,y+v)-I(x,y)]^2 $
其中 window function 可以使用加權函數、高斯函數
利用泰勒展開式對$I(x+u,y+v)$
其中一階近似為
將一階近似帶入 harris corner 公式
最終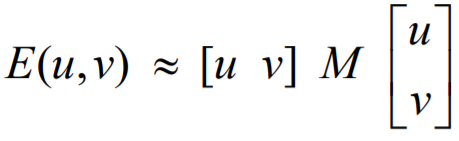
其中 M 是一個 2x2 的矩陣用來計算影像導數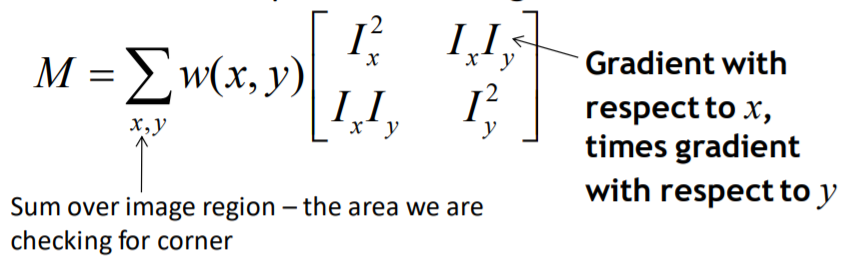
M 是對稱矩陣,求其特徵值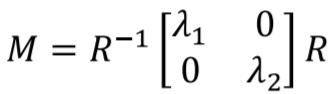
可以把矩陣 M 想像成是一個橢圓型,其中它的軸長是$\lambda_1 , \lambda_2$,方向由 R 定義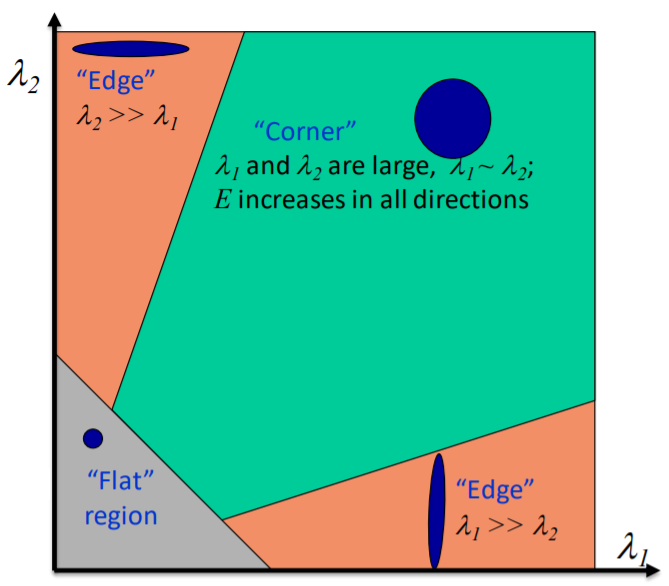
可以看到$\lambda_1 , \lambda_2$ 與影像的關係,而我們只關心 corner 的地方,試著將 corner 位置的值透過一個公式過濾出來
設計邊緣響應函數:
${\theta} = det(M) - {\alpha}trace(M)^2 = {\lambda_1}{\lambda_2}-{\alpha}({\lambda_1}+{\lambda_2})^2$
快速逼近法:
- 避免計算特徵值
- ${\alpha}是常數,範圍可選在[0.04,0.06]之間$
note
- det:Determinants,在矩陣上計算得到純量
- trace:trace,矩陣對角線上的總和
Harris corner 特性
- 參數$\alpha$對角點檢測的影響:加大$\alpha$值,減少角點檢測數量;降低$\alpha$值,增加角點數量
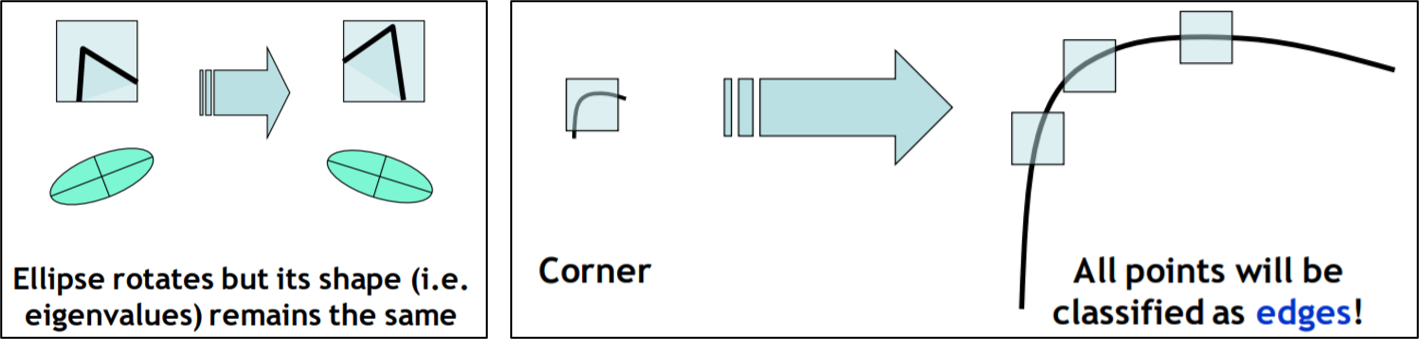
- 具有旋轉不變性,但沒有尺度不變性,視野範圍內看到的角點,放大視野範圍後會變成 edge
特徵檢測器相關論文
- Hessian & Harris [Beaudet ‘78], [Harris ‘88]
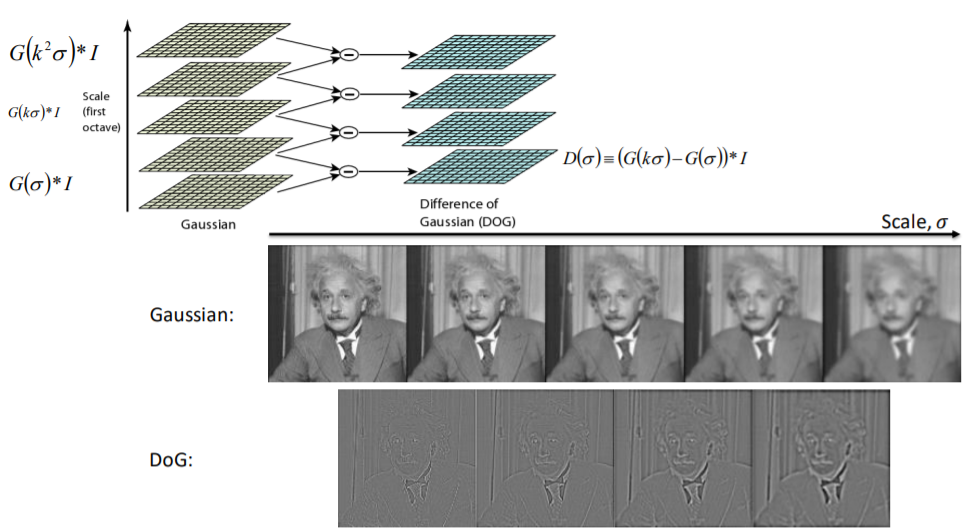
- Laplacian, DoG [Lindeberg ‘98], [Lowe ‘99]
- Harris-/Hessian-Laplace [Mikolajczyk & Schmid ‘01]
- Harris-/Hessian-Affine [Mikolajczyk & Schmid ‘04]
- EBR and IBR [Tuytelaars & Van Gool ‘04]
- MSER [Matas ‘02]
- Salient Regions [Kadir & Brady ‘01]