edge 的重要性
- 大部分的形狀等資訊可以從邊緣分析出來
- 用 edge 來提取資訊、辨識物件
- 回復幾何形狀與消失點(vanishing point)
edge 產生原因
- 表面法向不連續性(Surface normal discontinuity):區塊內看到多個不同角度的表面
- 深度不連續性 (Depth discontinuity):由物體前後距離不一所產生邊緣
- 表面顏色不連續性 (Surface color discontinuity):物體改變顏色,例如材質顏色改變
- 亮度不連續性 (Illumination discontinuity):陰影,光線亮度變化

邊緣檢測在一階微分應用
edge detection Using First/Second Derivative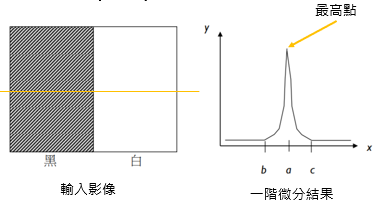
透過一階微分找出亮度變化大的地方
First Derivative
1D function: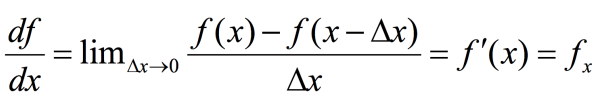
2D function:
轉換成 2D mask/filter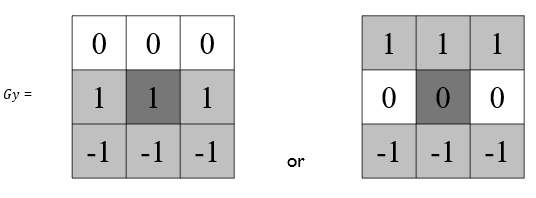
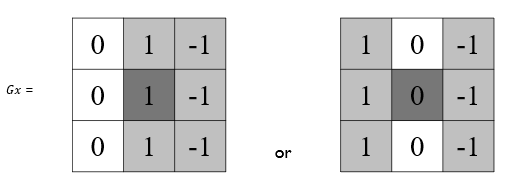
- gradient vector:對 x,y 方向進行偏微分,也就是用上述兩個 Gx, Gy 的 mask 個別對影像進行 convolution
- gradient magnitude:透過 x,y 方向梯度的加總得到最終梯度強度
- gradient direction:gradient vector 中 gradient 變化量最大的角度
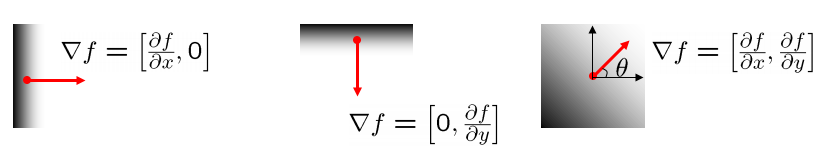
noise 對 edge detection 的影響
- noise 對邊緣檢測的影響不大
- 若有較大的影響可以考慮先對影像進行平滑運算
- Median filter
- Gaussian filter
- Bilateral filter
Tradeoff:影像模糊度越強,noise 越少,但 edge 也會被模糊掉
edge detector
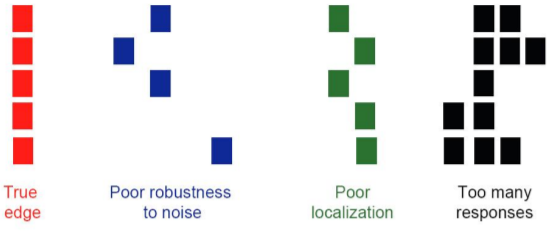
好的 edge detector 應避免這些事情發生
- Poor robustness to noise:對 noise 抵抗能力低
- Poor localization:與真實 edge 位置仍有小幅度差距
- Too many responses:檢出太多不必要 edge
Sobel edge detector
Sobel Operator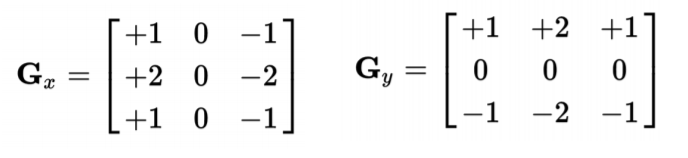
由高斯平滑 + 一階微分 組成
gradient magnitude & gradient direction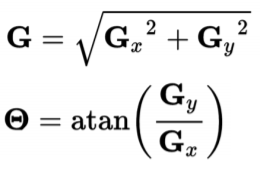

缺點
- 準確率差,誤判率高
- 對 noise 敏感
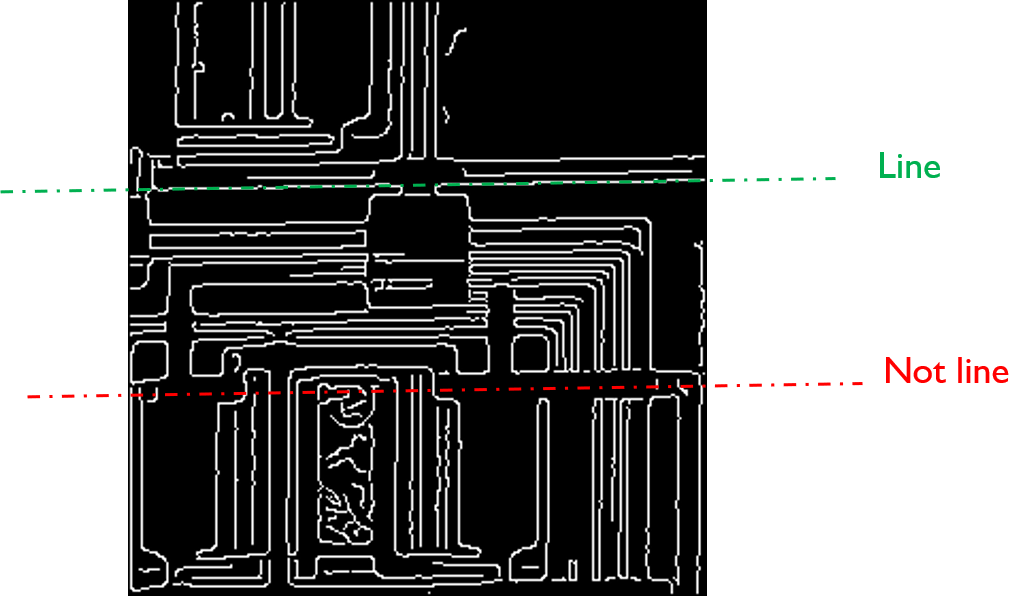
Line Detection
直線是一個很常見的特徵,例如在建築物、道路、零件電路板等都看得到
從 edge 資訊更進一步找出直線
Naïve method
對影像中的 edge 點任取兩個點,檢查在此點形成的線上是否有其他 edge 點
當點數量大於一定值時,視為真正的直線
缺點:
- 時間複雜度為$ O(N^2) $ ,N 為 edge 數量
Hough transform
與蠻力法相似,用投票的方式來找出合適的線段
但不同的地方在於使用 hough space 將直線透過另一種公式做轉換
Hough space
直線方程式
$ y=ax+b $(1)
但這個方程式(1)不能表示垂直的線段
$ r = xcos \theta + ysin \theta $ (2)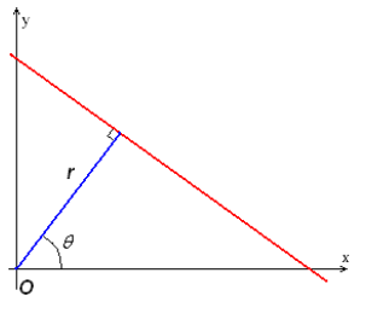
因此由公式(2)可以簡單的改變$ \theta $ 值組合出多種不同角度的直線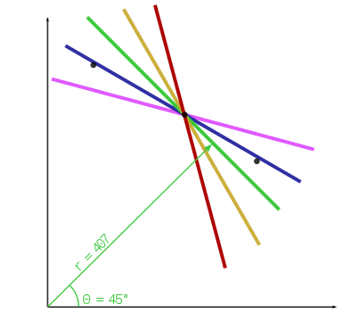
單個 edge 點(x,y)在$ [r,\theta] $ hough space 下所呈現多條直線的結果為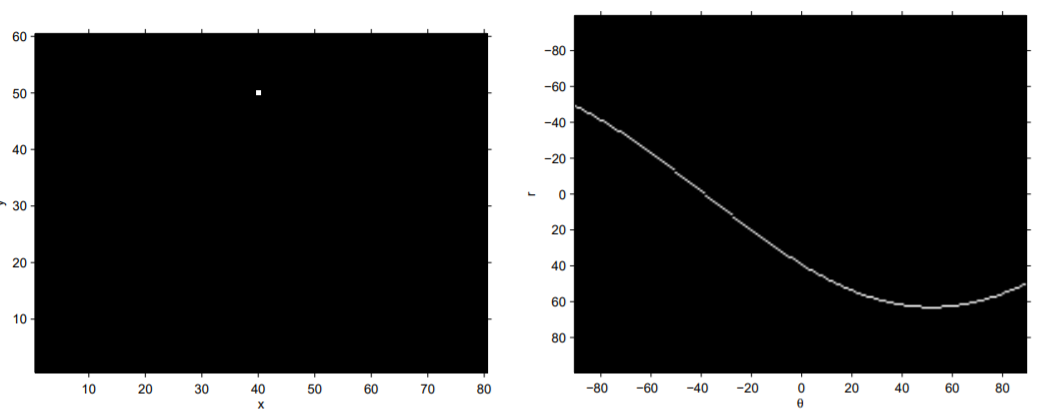
可以看到單個點在$ [r,\theta] $空間下畫出一條彎曲線
加上不同 edge 座標點,可以在 hough space 下畫出多條彎曲線
並且有疊加交點,而此交點正好是兩點所形成的直線$ [r, \theta] $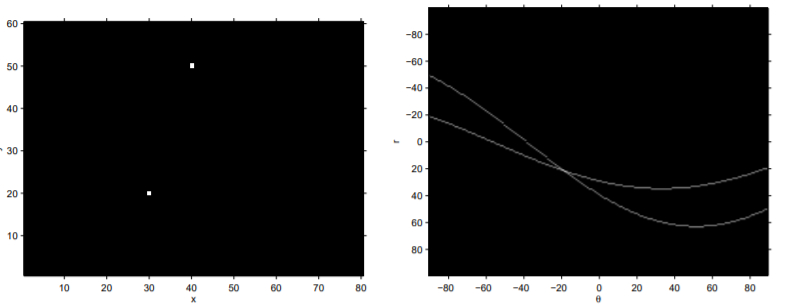
可篩選交點數較多的點為真實直線,也可以篩選指定直線角度範圍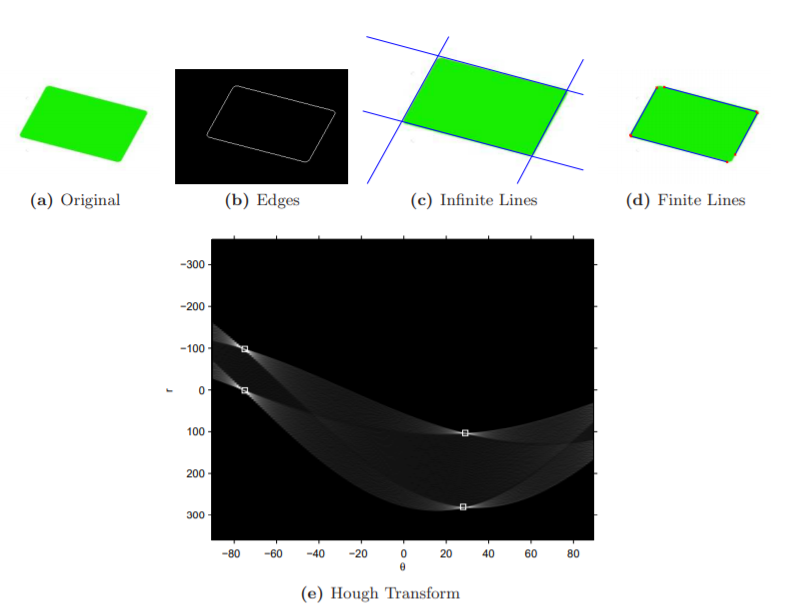
優點:
- 概念簡單,好實現
- 相同概念也可以用在檢測圓形
缺點:
- 只得到直線角度資訊,沒有直線長度資訊
補充
消失點 vanishing point

消失點是三維空間中所有平行線相交的交點。
消失點的應用在檢測道路上有很大的幫助,在二維影像中車道最終會在消失點相交,但真實空間的車道是平行的。
透過 edge 尋找消失點,進行道路檢測。